autor: Paweł Jochymek

Co to jest maswerk? Zaproponuję definicję z Wikipedii – dekoracyjny, geometryczny wzór architektoniczny odkuty z kamienia lub zrobiony z cegieł, używany do wypełnienia górnej części gotyckiego okna, przeźrocza, rozety, itp. Występuje także jako dekoracja ścian, murów, wimperg, blend. Taki element jest nazywany ślepym maswerkiem.
Jedynym miejscem, gdzie można w Starym Sączu je znaleźć jest oczywiście klasztor klarysek, a dokładniej Kościół Trójcy Świętej. Wchodząc na dziedzinie klasztorny możemy dostrzec gotyckie okna z witrażami, w których górnej części znajdują się poszukiwane maswerki.

Rysunek dwóch maswerków wykonany podczas wycieczki artystyczno-naukowej uczniów Krakowskiej Szkoły Sztuk Pięknych prowadzonej przez prof. Władysława Łuszczkiewicza w 1891 roku.

Nie są one może nadzwyczajnie atrakcyjne, w porównaniu z tymi z innych części świata, ale nie o atrakcyjności chciałbym tutaj napisać.

             

Patrząc na te wspaniałe geometryczne wzory, zastanawiałem się jak one zostały skonstruowane? Jakim metodami, nie mając komputera i programów graficznych, udawało się ówczesnym architektom osiągnąć takie wspaniałe rezultaty? Okazuje się, że maswerki są tworzone wyłącznie z łuków okręgów. Wszystkie te cudowne działa można narysować za pomocą cyrkla i linijki. Wracamy zatem do korzeni geometrii, do Euklidesa i do zasad, które postulował w swoich „Elementach”.
W tej pracy chciałbym przedstawić przykłady geometrycznych konstrukcji starosądeckich maswerków. Można je wykonać tradycyjnie na kartce papieru za pomocą cyrkla i linijki lub bardziej współcześnie – komputerowo. Do tworzenia konstrukcji użyłem programu Geogebra. Jest to darmowy, polskojęzyczny program wspomagający naukę matematyki i geometrii. Korzystając z niego będę trzymał się euklidesowej zasady cyrkla i linijki, lecz dodatkowo w niektórych sytuacjach będę podawał polecenia, które można wpisać do pola wprowadzania.

Zaczniemy od konstrukcji najbardziej charakterystycznego elementu w stylu gotyckim – od ostrołuku. Wszystkie nasze okna zakończone są ostrołukami.

rys. 1	rys. 2	rys. 3

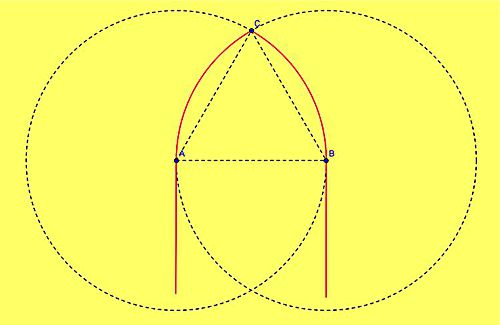	Ostrołuk klasyczny – powstaje na bazie trójkąta równobocznego. Rysuję odcinek AB, następnie dwa okręgi o środkach w punktach A i B i promieniu AB. Miejsce przecięcia (punkt C) tworzy wierzchołek ostrołuku. Rysuję łuki AC i BC. Dodatkowo narysowałem dwie półproste prostopadłe do AB i całość pokolorowałem na czerwono.
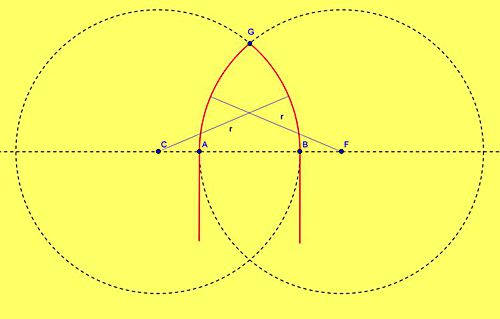	Oczywiście nie wszystkie ostrołuki są w ten sposób skonstruowane. Istnieją ostrołuki smukłe, w których środki łuków znajdują się na zewnątrz otworu okiennego – tutaj w punktach C i F.
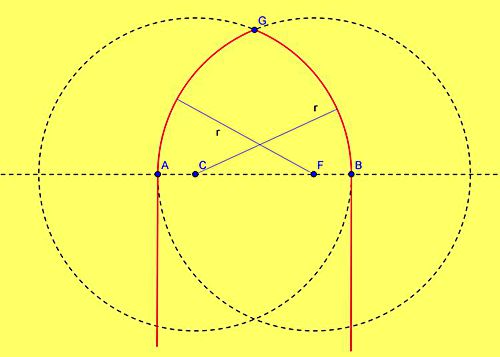	Lub ostrołuki szerokie, gdzie środki łuków znajdują się wewnątrz otworu okiennego (punkty C i F)

Wszystkie trzy okna są podzielone na dwie części. Są to tzw. okna dwudzielne. Każda część zakończona jest małym ostrołukiem. Nad ostrołukami wpisane są kolejne charakterystyczne elementy dekoracyjne. Na pierwszym rysunku jest to pięcioliść wpisany w okrąg; na drugim trójliść wpisany w trójkąt wypukły (trójkąt Releaux), a na trzecim trójliść wpisany w okrąg. Ostrołuki wewnętrzne wykończone są bardzo często występującymi, charakterystycznymi zdobieniami, a w maswerku na rys 3 mamy dodatkowo, poniżej, kolejne motywy zdobnicze.

Zajmę się konstrukcją podziału okna na dwie części, stworzenia wewnętrznych ostrołuków i wpisaniu okręgu stycznego do tych ostrołuków.

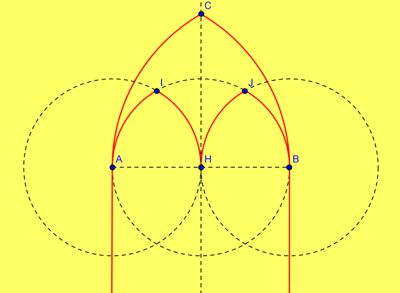	W utworzonym ostrołuku klasycznym znajduję punkt H, który jest środkiem odcinka AB. Możemy to zrobić konstrukcyjne rysując symetralną odcinka AB lub wpisując w pole wprowadzanie polecenie: PunktŚrodkowy[A,B] Rysuję teraz trzy okręgi o środkach A, B, H i promieniu AH. Punkty I i J tworzą wierzchołki wewnętrznych ostrołuków. Rysuję i koloruję odpowiednie łuki.
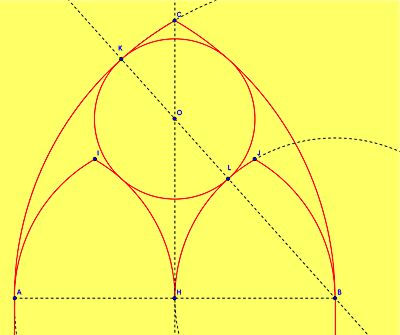	W jaki sposób znaleźć środek okręgu O i jego promień? W tym przypadku sprawa jest prosta. Narysowany okrąg jest styczny w punkcie K do dużego ostrołuku i w punkcie L do małego ostrołuku. Punkt B jest środkiem obu okręgów na bazie, których powstały ostrołuki.
	Zgodnie z twierdzeniami 11 i 12 Euklidesa z księgi III „Elementów” Jeśli okręgi są styczne do siebie zewnętrznie (tw. 11) lub wewnętrznie (tw. 12) to prosta przechodząca przez ich środki przechodzi przez ich punkt styczności. (patrz rysunek obok)
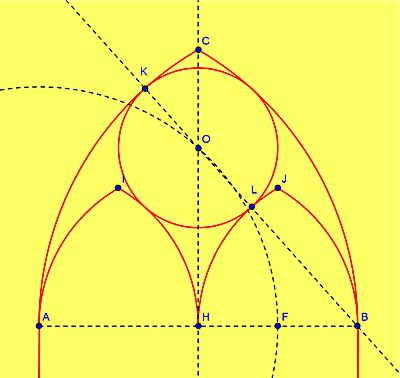	Na rysunku widać, że odcinek BK = AB (promień dużego okręgu), a BL = ½ AB (promień małego okręgu). Wynika z tego, że KL = ½ AB. Ponieważ jest to średnica (przechodzi przez punkt O) więc odcinek OL = ¼ AB – promień szukanego okręgu. Środek O będzie punktem przecięcia okręgu o środku A i promieniu ¾ AB z prostą CH. Konstrukcja: znalazłem środek odcinka HB (konstrukcja symetralnej lub polecenie PunktŚrodkowy[B,H]) i narysowałem okrąg o środku A i promieniu AF.
	Jednak nasz maswerk jest nieco inny. Okrąg jest dużo większy, a wewnętrzne ostrołuki nie mają wspólnej podstawy z ostrołukiem dużym.
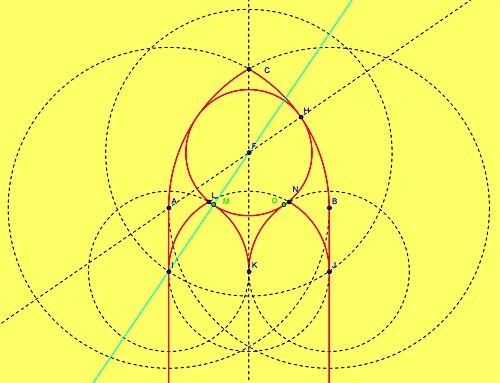	Rysuję ostrołuk ABC na bazie trójkąta równobocznego. Znajduję jego środek ciężkości – punkt F. Rysuję prostą AF i wyznaczam punkt H. Rysuję okrąg o środku F i promieniu FH. Musze teraz znaleźć punkty I oraz J, potrzebne do skonstruowania wewnętrznych ostrołuków. Punkty M i O są punktami styczności ostrołuków z okręgiem. Zauważmy, że długość IM = połowie AB ,a długość FM = FH (promień okręgu). Należy zatem narysować okrąg o środku F i promieniu o długości FH + ½ AB. Polecenie: Okrąg[F,odcinek[F,H]+odcinek[A,B]/2]. Po wyznaczeniu punktów I oraz J rysuję wewnętrzne ostrołuki.
Przedstawię teraz konstrukcją pięcioliścia wpisanego w okrąg.
	Dzielę okrąg na 10 równych części. Wykorzystam metodę podaną przez Herona z Aleksandrii. Mam dany okrąg o środku A. Wyznaczam punkt B na okręgu. Rysuję prostą AB i prostą prostopadła do AB przechodzącą przez punkt A. Wyznaczam punkt C. Znajduję środek odcinka AC (Punktśrodkowy[A,C]). Rysuję okrąg o środku D i promieniu AD. W przecięciu tego okręgu z odcinkiem DB otrzymałem punkt E. Odcinek BE jest bokiem dziesięciokąta. Zaczynając od punktu B rysuję okręgi o promieniu BE.
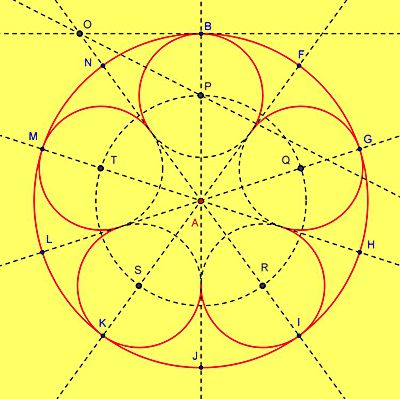	Mamy podzielony okrąg na 10 części. Rysuję proste AF, AG, AH, i AI. Konstruuję prostą prostopadłą do AB przechodzącą przez punkt B i wyznaczam punkt O. Konstruuję dwusieczną kąta AOB (polecenie: Dwusieczna[A,O,B]). Punkt P jest środkiem jednego z okręgów pięcioliścia. Rysuję okrąg AP, znajdując pozostałe środki okręgów (Q, R, S, T). Rysuję i koloruję odpowiednie łuki.
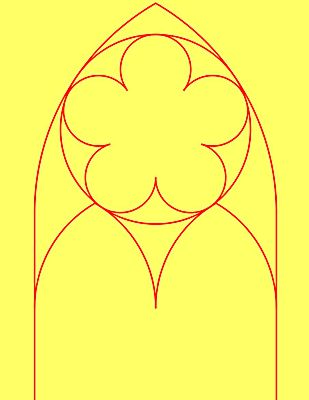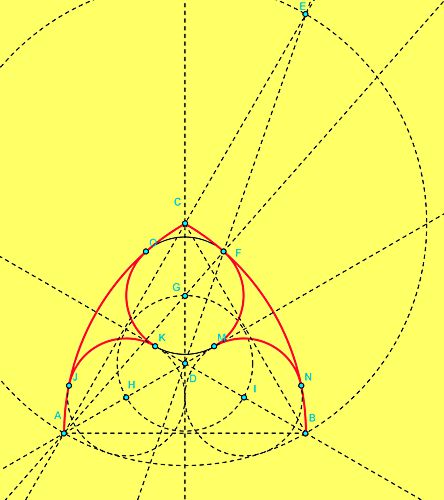	Pozostała jeszcze konstrukcja charakterystycznych ozdób w wewnętrznych ostrołukach. Rysuję boki trójkąta równobocznego, na którym oparty jest ostrołuk. Konstruuję symetralne jego boków i znajduję punkt ich przecięcia (punkt D). Rysuję prostą AC i okrąg o środku C i promieniu AC i znajduję punkt E. Rysuję prostą DE. Punkt F jest przecięciem tej prostej z łukiem BC. Rysuję prostą AF i znajduję punkt G, który jest środkiem okręgu o promieniu GF. Punkty H oraz I okręgów o promieniu długości GF. Polecenie: okrąg[H,GF] oraz okrąg[I,GF]. Zaznaczam punkty przecięcia okręgów, rysuję i koloruję odpowiednie łuki.
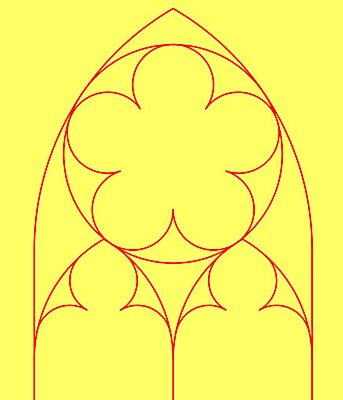	Tak przedstawia się cały skonstruowany maswerk

1	czytaj dalej