autor: Paweł Jochymek

Starosądeckie maswerki (cz. 2)
Piękno jest bezpośrednim wyrazem doskonałej
zgodności z prawidłami matematyki
Otto von Simson


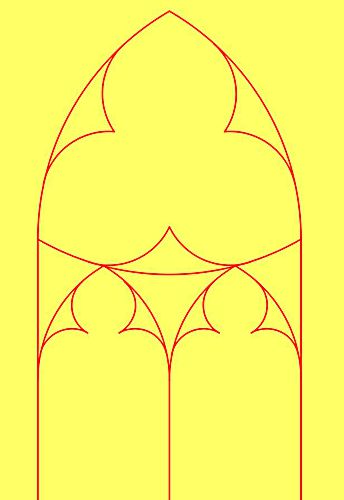
Zajmę się teraz drugim maswerkiem.
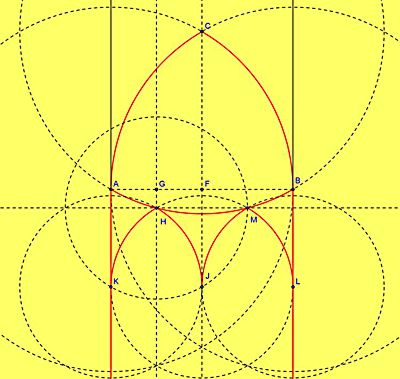Konstruuję klasyczny ostrołuk jak w przykładzie 1. Dodatkowo rysuję okrąg o środku C i promieniu AC. Odpowiednie łuki tworzą trójkąt wypukły ABC (w którego wpiszę trójliść). Teraz tworzę dwa wewnętrzne, małe ostrołuki. Znajduję punkt F – środek AB, oraz punkt G – środek AF. Konstruuję prostą CF oraz prostą prostopadłą do AB przechodzącą przez punkt G. Punkt H jest wierzchołkiem wewnętrznego ostrołuku. Aby znaleźć środki łuków tych ostrołuków (K i J) konstruuję okrąg o środku H i promieniu AF. Rysuję okrąg o środku K i promieniu KH oraz okrąg o środku J i promieniu JH. Wyznaczam punkt L oraz M. Rysuję okrąg o środku L i promieniu LM. Koloruję odpowiednie łuki na czerwono.
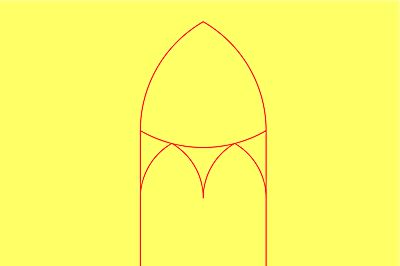Ukrywam linie pomocnicze i otrzymuję taki oto maswerk. Brakuje jeszcze trójliścia wpisanego w wypukły trójkąt.
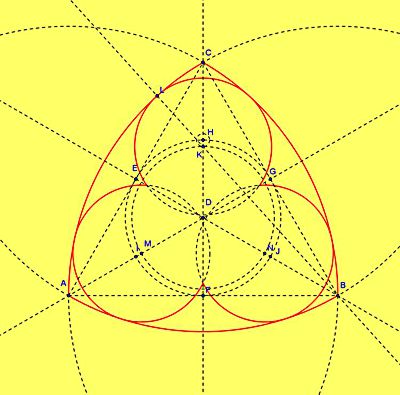Przedstawię konstrukcję trójliścia, który trzeba wpisać w dany trójkąt wypukły. Mam trójkąt wypukły ABC. Łączę punkty ABC tworząc trójkąt równoboczny. Rysuję symetralne boków i wyznaczam punkt D. Symetralne przecinają boki trójkąta w punktach E, F, G. Rysuję okrąg o środku D i promieniu DE. Okrąg przecina symetralną CD w punkcie H. Dzielę promień okręgu DH na 12 części i rysuję okrąg o środku H i promieniu 11/12 DH. (Uwaga! Konstrukcja podziału odcinka na 12 części jest pracochłonna więc wykorzystałem polecenie: okrąg[H,odcinek[H,D]*11/12].
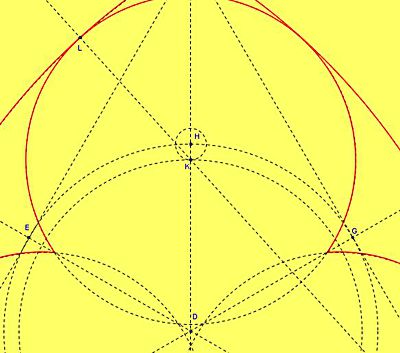Wyznaczam punkt K, który jest środkiem jednego z okręgów trójliścia. Prowadzę prostą BK i wyznaczam punkt L (KL jest promieniem okręgu). Rysuję okrąg o środku D i promieniu DK wyznaczając punkty M i N – środki pozostałych okręgów. Rysuję i koloruję właściwe łuki.




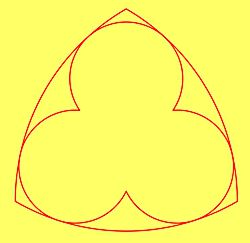Po usunięci linii pomocniczych otrzymujemy piękny trójliść. Jeszcze tylko drobna kosmetyka – usunięcie łuków z narożników trójkąta. Oraz dorysowanie ozdób w wewnętrznych ostrołukach (jak w konstrukcji maswerku nr 1) i mamy gotowy maswerk nr 2.


wstecz 2 czytaj dalej