autor: Paweł Jochymek
Starosądeckie maswerki (cz.3)
Piękno jest bezpośrednim wyrazem doskonałej
zgodności z prawidłami matematyki
Otto von Simson
zgodności z prawidłami matematyki
Otto von Simson
Przejdę do maswerku z rys 3.
 | Po wstępnej korekcji zniekształceń trapezowych trzeciego zdjęcia dokonałem analizy geometrycznej. Ostrołuk główny, jak i ostrołuki wewnętrzne są zbudowane na bazie trójkąta równobocznego. Jednak podstawy ostrołuków wewnętrznych są nieco obniżone w stosunku do podstawy ostrołuku głównego. |
 | Rysuję odcinek AB (szerokość okna – podstawa ostrołuku). Konstruuję okręgi o środku A oraz B i promieniu AB. Wyznaczam punkt C. Konstruuję prostopadłą do AB przechodzącą przez C. Z analizy geometrycznej wynikało, że podstawy wewnętrznych ostrołuków znajdują się od wierzchołka C w odległości równej szerokości okna. Zakreślam więc okrąg o środku C i promieniu AC. Znajduję punkt D. Konstruuję prostopadłą do CD przechodzącą przez D i kolejno prostopadłe do powstałej prostej przechodzące przez A i drugą przez B. Odcinki ED i EF są podstawami wewnętrznych ostrołuków. Następnie rysuję okręgi o środkach E, D i F i promieniu ED znajdując punkty G i H – wierzchołki wewnętrznych ostrołuków. Koloruję odpowiednie łuki. |
 | 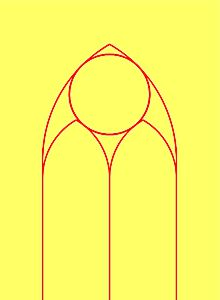 Muszę teraz podzielić odcinek EF na 10 części i narysować okrąg o środku E i promieniu 0,8 EF. Można ten podział zrobić konstrukcyjnie, ale ja posłużę się poleceniem: Okrąg[E,0.8*EF]. Znajduję punkt I, który jest środkiem szukanego okręgu. Konstruuję prosta EI znajdując punk styczności J z małym ostrołukiem i rysuję okrąg o środku I i promieniu IJ. Po usunięciu linii pomocniczych i dorysowaniu środkowego ramienia okna otrzymałem taki maswerk. |
 |  Mam dany okrąg o środku A. Na okręgu zaznaczam punkt B i dzielę okrąg na 6 równych części (rysuję okrąg o środku B i promieniu AB; otrzymuję punkty C i D, które są środkami kolejnych okręgów itd.; otrzymuję punkty E, F oraz G). Rysuję trójkąt CDG oraz proste BA, CA i DA. Punkty H, I, J tworzą środki okręgów tworzących trójliść. Koloruję właściwe łuki. |
 |  Wykonam teraz ozdoby w małych ostrołukach. Łączę wierzchołki ostrołuku. Rysuję symetralną AB oraz okrąg o środku B i promieniu 2/3 AB. Punkt I jest środkiem FH. Rysuję okrąg o środku B przechodzący przez punkt I; na boku BC znajduję punkt J. Z punktu I zakreślam okrąg o promieniu IA. Punkt K jest przecięciem tych okręgów. Rysuję i koloruję odpowiednie łuki. Analogicznie wykonuję ozdoby po drugiej stronie ostrołuku. |
 | Zajmę się teraz najniżej położonymi ozdobami w wewnętrznych ostrołukach. Składa się on z jednego prawie okręgu oraz dwóch ćwierćłuków. Wszystkie elementy są zbudowane na okręgach o promieniu ¼ szerokości okna. Wszystko u góry zwieńczone jest jeszcze łukiem. Z punktu H kreślę okrąg o promieniu ¼ AB. Znajduję punkt O, który jest środkiem okręgu o promieniu OH. Rysuję okrąg o środku C i promieniu AB. Punkt O oraz środki ćwierćłuków S i T tworzą trójkąt równoboczny o boku ½ AB. Aby znaleźć te punkty wystarczy zakreślić okrąg o środku O i promieniu równym wysokości trójkąta OST. Skorzystam z polecenia okrąg[O,sqrt(3)/4*AB]. Znajduję punkt R i konstruuję prostopadłą do prostej HO i przechodzącą przez R. Aby znaleźć punkty S i T rysuję okrąg o środku O i promieniu ½ AB. Z punktów S i T zakreślam okręgi i koloruję odpowiednie łuki. |
 Analogicznie postępuję z drugim ostrołukiem. |  A tak przedstawia się całość. |
 wstecz wstecz | 3 |
